Number Theory and Cicadas
Introduction
Periodic Cicadas, which belong to the genus Magicicada, are a species of insects in North America. Cicadas are well known for their long and unique life cycles. The entire population of billions of insects lies dormant in the ground for 13 or 17 years before emerging nearly simultaneously. They live above ground only for a few weeks - just enough time to mate, reproduce, and die. There are two groups of Cicadas - one which emerges every 13 years and another which emerges every 17 years.
This year, in 2024, both the 13 and 17 year Cicadas have emerged. Although I don’t live in the Eastern United States, I’m well aware of their presence through news and social media. I had never looked much into Cicadas before now, and I was curious to learn more about them.
Of initial interest to me was their long dormancy period - 13 or 17 years is a long time to spend underground! More specifically, however, I noticed that both broods of Cicadas have life cycles which are prime numbers. Was this a pure coincidence? Or is there some evolutionary advantage to emerging every prime number of years?
It should not be surprising that Cicadas are well studied, and there are many hypothesis as to why their lifecycles are prime numbers. We’ll explore some of these here, as they are rooted in some basic, yet beautiful, number theory.
Don’t Compete
The first hypothesis for this prime number emergence claims that Cicadas are most successful when they aren’t competing for resources with the other brood. In fact, the two broods of Cicadas will emerge together only every 221 years! You’ll notice that 221 = 13 * 17. This is no coincidence - the least common multiple of two prime numbers is always exactly equal to their product.
Speaking mathematically, this fact corresponds to the following claim:
Theorem: Suppose that \(p,q\in\mathbb{N}\) and \(p\) and \(q\) are prime numbers. Then the least common multiple of \(p\) and \(q\) is \(pq\).
For the following proofs, note that \(a|b\) means that \(a\) divides \(b\). Or, more formally, there exists an integer \(k\) such that \(ak = b\). Additionally, note that \(\text{gcd}(a, b)\) corresponds to the greatest common divisor - the largest number that divides both \(a\) and \(b\) exactly. Likewise, the \(\text{lcm}(a, b)\) corresponds to the least common multiple - the smallest number that is divided by \(a\) and \(b\) exactly.
Lemma: Let \(a,b\in\mathbb{N}\). Then \(\text{gcd}(a,b)\cdot\text{lcm}(a,b) = ab\).
Proof of Lemma: Let \(a,b\in\mathbb{N}\), and let \(d = \text{gcd}(a, b)\). Thus, \(\exists, a_0, b_0\in\mathbb{N} : a = d\cdot a_0, b = d\cdot b_0\). Let \(m = \frac{ab}{d}\). Our goal is to show that \(m\) is the \(\text{lcm}(a,b)\). Let us begin by proving that \(m\) is a multiple of \(a\) and \(b\).
Then, consider the following
\[\begin{align} m &= \frac{ab}{d} \\ &= \frac{d a_0 b}{d} \\ &= a_0 b \end{align}\]Thus, \(b\mid m\). Similarly, consider the other substitution
\[\begin{align} m &= \frac{ab}{d}\\ &= \frac{a d b_0}{d}\\ &= a b_0 \end{align}\]Likewise, \(a\mid m\). Therefore, we can conclude that \(m\) is a multiple of \(a\) and \(b\).
Next, let us prove that \(m\) is the least common multiple of \(a\) and \(b\). Define a new value \(c\) which is any common multiple of \(a\) and \(b\). If we prove that \(m \le c\), then \(m = \text{lcm}(a,b)\). Then \(\exists x, y\in\mathbb{N} : c = ax = by\).
Consider the value of \(\frac{c}{m}\). If \(\frac{c}{m}\in\mathbb{Z}\) then \(m \le c\). Consider the following
\[\begin{align} \frac{c}{m} &= \frac{cd}{ab}\\ &= \frac{c(as + bt)}{ab}\\ &= \frac{cas}{ab} + \frac{cbt}{ab}\\ &= \frac{cs}{b} + \frac{cb}{a}\\ &= \frac{bys}{b} + \frac{axt}{a}\\ &= ys + xt \end{align}\]For the second step, note that the \(gcd\) can always be written as a linear combination as per Bézout’s identity, and that \(s, t\in\mathbb{Z}\). Since \(y, s, x, t\in\mathbb{Z}\), then \(\frac{c}{m}\in\mathbb{Z}\) and hence \(m \le c \implies m = \text{lcm}(a,b).\blacksquare\)
Proof: Suppose that \(p, q\in\mathbb{N}, p \ne q\) and both are prime. Then \(\text{gcd}(p, q) = 1\). Then, from the lemma, \(\text{gcd}(p, q)\cdot\text{lcm}(p, q) = pq \implies \text{lcm}(p, q) = pq\). \(\blacksquare\)
Don’t Feed
Another hypothesis notes that Cicadas could become a regular, predictable food source for predators. Cicadas have virtually no inherent defenses, and instead rely on their short lifetime and massive numbers to avoid extinction. However, in order for a certain predator to regularly rely on Cicadas for food, they would need to always be of hunting age at the same time that the Cicadas emerge.
Intuitively, it makes sense that choosing a prime-number lifetime \(n\) would be advantageous for prey since predators would not be able to immediately divide into the prey’s life cycle without having a lifespan of 1 or \(N\) years. However, this property falls apart once you consider that multiples of primes are not prime. A lifespan of 7 years, for example, would mean another brood would emerge after 14 years, which would be advantageous to predators with a two year life cycle. In short, some primes are better than others for this purpose.
To model this, we can define a stepwise function \(f(n, N)\) where \(N\) defines the lifespan of the predator and \(n\) defines the lifespan of the pray. We can then assign a score to the respective values of \(n\) and \(N\) as such
\[f(n, N) = \begin{cases} 1& n = N\\ \frac{1}{N} & n < N\\ \frac{1}{2^{k-1}} & n=kN : k\in\mathbb{Z}\\ \frac{1}{N2^{(n/N) -1}} &\text{otherwise} \end{cases}\]If you maximise these values for reasonable values of \(n\) and \(N\), you’ll find that predators are most likely to chose a value of \(N=4\). And (drumroll), prey are likely to choose a value of \(n = 17\), followed by a secondary local minimum of \(n = 13\)!
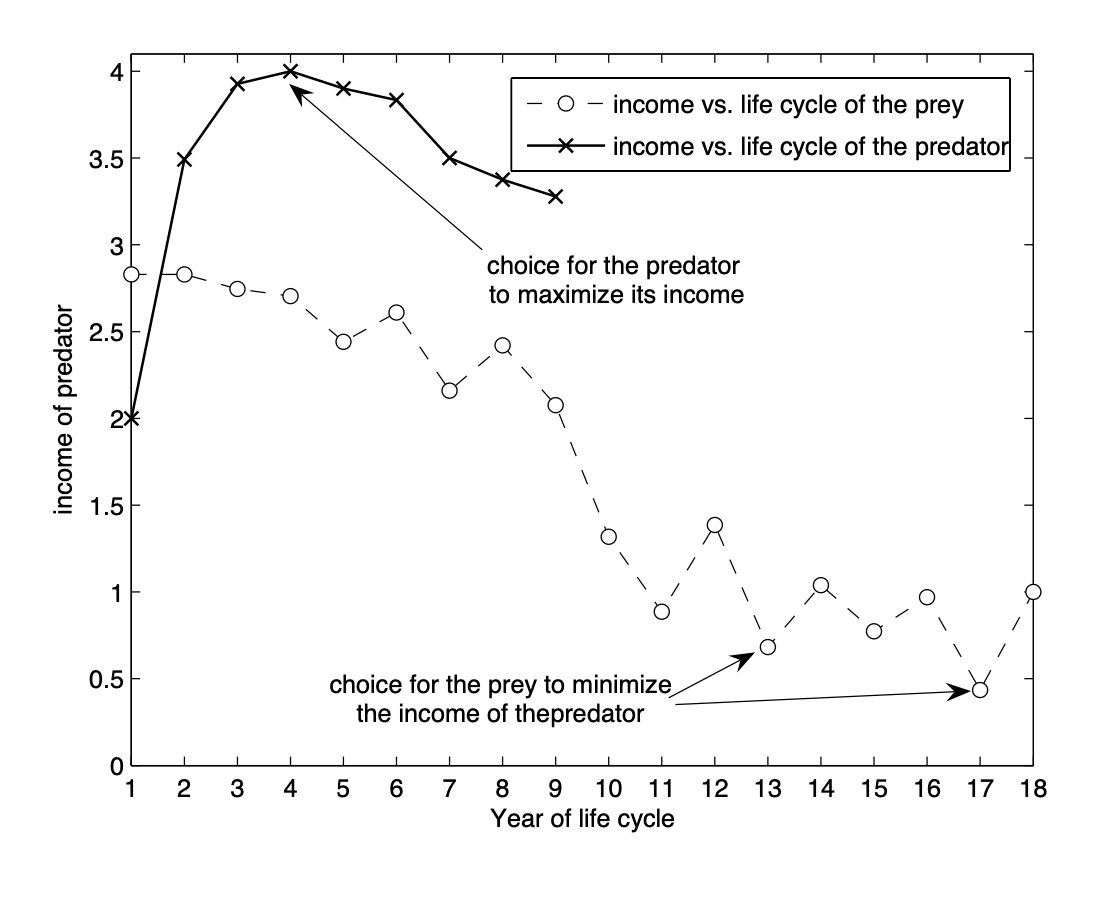 Image courtesy of Shi Chen, North Carolina State University
Image courtesy of Shi Chen, North Carolina State University
These findings are also supported by experimental evidence. The insect Mud dauber, for instance, is one of the Cicadas most prolific predators. And, believe it or not, it has a lifecycle of 4 years!
Closing Thoughts
Nature is cool, and it’s fascinating to think about how processes like natural selection can lead to the emergence of properties from number theory.
On a more existential note, however, imagine yourself as a Cicada. You spend nearly your whole life underground, gnawing on the roots of trees only to emerge for a brief period of time and experience the world before reproducing and dying. If Cicadas were capable of abstract thought, I wonder what they would think of this time above ground. Would it appear all too short for them, or would they appreciate the time they got to experience flight? Would they even have a concept of how short their time above ground was?
Food for thought.